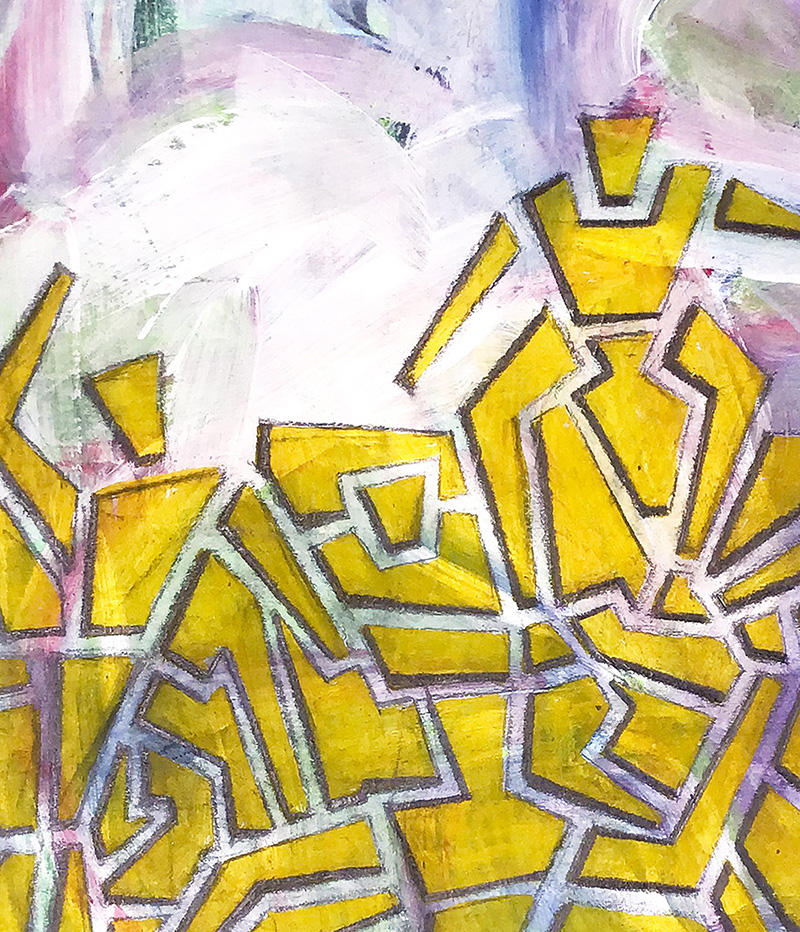A striking example of this is a topic I remember we discussed sometime in the past.
For some unknown reason and for some unknown length of time, we have been in a habit of symbolizing the "dot" as a circle. When it is wanted to be represented in three dimensions, it is symbolized with a sphere, a balloon or a game ball.
The dot has several meanings or uses: a sign indicating the end of a sentence, marks placed around letters in various alphabets to produce new letters, a specific location, moment or aspect, decimal, thousand, part, time, sound etc separator inserted between numbers, notes and the like. But none of their descriptions tell that a point is a circle. Is this habit or tendency within us a remnant of false narratives? Just like when we say "border" a line comes to our mind. However, the border is not a line, but a strip where two things meet or where one ends and the other begins, sometimes clear but often ambiguous.
So, what is a dot, really?
Any formed round spot is also called by the thing we mostly are used to: "dot". We see that such forms were also called "benek" in the Ottoman Turkish dictionary. Although it is used with different names as to its place of use in many other languages (such as "point", "dot", "full stop" and "period" in English), they are all the same dot; at least that's how they are used today. Therefore it cannot be argued that when used in a certain sense, its form is like this and, in another case, it is called like that. There are also expressions of "round sign" in modern dictionaries because in old printing systems and computer fonts, dots have often been created in the form of a circle for technical reasons. But actually, a dot is a stain created by a single stroke; anything more than that is something else. Therefore, if we take the most produced form as an example, none of the strokes we create on paper with a pen are round. For centuries, no writer, no poet, no scientist has tried to make the dot in a circular form when finishing their sentences. Because the dot is just a symbol, and when used as a symbol in writing systems, the only expectation is it be visible. It should be created in a single stroke and as tiny as possible. Imagine musicians trying to make dots in circle shapes while notating a composition… Having to darken it or make it larger so that it can be visible never changes what a dot actually is.
Dot and circle are separate concepts that have also been laid out since the foundations of philosophy. In philosophy and ancient symbols, there are concepts of "dot in the circle", "circulated dot" or "circumpunct". The concern in using a dot inside a circle is an attempt to explain or illustrate that the two are not the same thing. The dots, which we saw in ancient Egypt and Greece, of course, symbolized the very creation, god or divine consciousness and circles symbolized the living or perceptible zone, like the universe or the earth, while they when together symbolized the human being. Inevitably, these meanings were evolved and used again and again in later periods.
Leaving aside the circle here, the dot is known as the "closest to perfect", "simplest" and "least far from perfect" symbol. A process, that is, time, begins with a dot, that is, a perfect stroke, on a surface such as a blank piece of paper with nothing on it. That is, when there is no dot, there is no time. At the end of the process that begins with such a perfect movement, meaning is created on the white paper surface. You can also draw a line on paper—but we are talking about perfect; not only is the line far from perfect, it is also the sum of an infinite number of moments, each containing one dot, which when lined up compose the time.
In my Reflections series of paintings, I explain that meaning is created when people cover up the truth—a similar phenomenon. Human impulses, because they are just pulses, create time—also by interacting with each other—and add meaning to integrity in the space of nothingness.
Back to our topic…
Well, if the dot is the trace left by a stroke, this means "sometimes we may not see this trace". So how would we know that a dot exists on paper that is invisible to the eye? If we cannot see or detect something, can we talk about its existence? If the dot is created with a material, for example, a pencil, a residue of that material must be present on the surface. What if the point we cannot detect is in white color? What if there cannot be any residue, such as the ink of the pencil? Moreover, like the example always given; although fossils prove that a living thing existed, they are not proof that that creature exists now. Or, the fact that we cannot find fossils of living things that we cannot identify does not prove that those creatures never existed, nor does it show that they do not exist today. A trace created by a grain of dust on the surface is an ideal dot for us. But for a bacterium, it's a giant pit. Such mental exercises will lead each individual—seeking answers—to different views or conclusions depending on how they define the relevant elements of the question. That's why philosophers explain their discoveries in the most detailed ways and with a variety of methods so that what they reveal can be detected by everyone.
A phenomenon that we just call "a dot" can be so complex yet mind-expanding. In practice, it is natural for us to want to get away from all such complexities. But why can we not change the description of the dot and simplify it? The answer lies in the fact that it is one of the basic components of mathematics and geometry, as well as philosophical debates. The dot, or point, takes all the meanings we use in our daily lives from its meaning in mathematics. The uses in daily life are just mathematical symbolism—nothing else. Each digit or each number corresponds to a point on a specific axis, unlike expressions such as pi or 4/3. The decimal number 1.9 corresponds to a specific point, but when you add an infinite number of 9s to the right of it, it starts to correspond to a specific range depending on your definition of context, but it can never be as precise as the position of the number 2. Since we can add 9's an infinite number of times and get closer and closer to 2, but never reach it, we cannot talk about any width or length of 2. Therefore, a dot is not something that takes up space in space. This is why the point is considered dimensionless while three-dimension is exemplified as space, two-dimension as surface and one-dimension as line.
I am not an expert on philosophy; I do not see myself as having the authority to delve further into these issues. Here, I would like to return to the "points" that led me to the questions I mentioned in the introduction of this article.
There is no one who no longer accepts that the human brain's most efficient way of working and producing is through the neuronal pools that we describe as visual memory. Naturally, the most natural way to convey certain information is to use visual materials and add entertainment elements while doing this. However, in this process, both the drawbacks should be avoided and the opportunities it will bring should be evaluated well.
Attention should be paid to the symbolizations in the concepts, and if the subject is not known in detail, external expert support should be sought. Symbols should not be used as a means of entertainment but as a means of creating an enlightening or educational basis for inquiry and discussion. When this is done, with a single "stroke", awareness on other fields and concepts will be increased and countless doors will be opened to understand the intellectual plane—just like I tried to do in this text, based on the concept of "dot"…
In my works that I exhibited in my "My Timeless (Ill-Timed) Times" exhibition in 2012 with the term "reflections", I symbolized the integrity/indivisibility of the society, and basically expressed three phenomena: the ego impulses, the human embodiments driven by the ego impulses, and the obscurity and the consumption of the pure reality and of the nature by the human embodiments. The arithmetic balance enjoyed on canvases depends on the existence of all of the human embodiments.
The impulses (drives) that generate for the reason of being alive dismantle space and time. This disintegration caused by the interactions among the impulses turns the existence to understandable and makes the human an entity that questionize themselves. I contribute to the said questioning with the network theory that I have formulated on my own observations. On my thesis of "contingency and affectivity" (state of being adjacent and influencing), I express that the human, ironically, despite their said quizziness, legalizes a structure formed just by egos and, thereby, stretches and destroys the "array".
In a context where the word "array" can be translated into the daily language as a sequential table containing items that improve and assist one another, each element of the "array" –that is, the individuals- do, because they are just the elements of the array, own unique missions. However, actions required by those missions need specific amounts of radii. The radii cause individuals to depart from each other whereby what we call the society is formed.
As one can see, certain organs that belong to some groups of individuals of the array who tender crowdedness and turbulence are in extreme hustle setting up individuals' egotism at excessive levels. Some organs of some individuals, however, are dull, cannot find a room, or are wiped out, run over by an organ of a more dominant individual. Attempting to add required room in order to eliminate this situation may extinguish the balance, the society, because, with the existing state, individuals have built up a dynamic "network" among themselves and can perform their role with the help of others. This compulsory asymmetric contingency and affectivity, as a result, obscures and consumes the pure reality and the reality of nature.
The creation of the artworks contains a search for geometricizing the social pressures and rudeness. As a consequence of the search, arithmetic bursts as edges of the objects are applications that I have dared after calculations and try-outs in a manner not ever done before. While I paint the society-individual formation I observe in a constructive perception and in a conventional attitude, I apply the white color, which is not acknowledged as a color at all, in a wild manner. Thereby, my artworks within the concept of my thesis convey how much at a reverse position of the general opinion I have arrived.
